


§ 58. Корреспондирующие наблюдения метеоров. Базис
Корреспондирующие наблюдения метеоров проводятся одновременно из двух достаточно удаленных точек земной поверхности. Линия, соединяющая оба пункта наблюдений, называется базисом. Базис обычно выбирается равным 30-40 км. Чем больше базис, тем больше параллактическое смещение пути метеора на небесной сфере, но тем менее вероятность наблюдений одного и того же метеора из обоих пунктов.
Наблюдения можно производить кАк визуально, так и фотографически. Последний метод дает более точные результаты, вплоть до того, что можно определить радиант на основании двусторонних наблюдений только одного метеора. При наблюдениях приходится очень точно отмечать моменты полета метеоров, так как отождествление производится на основании совпадения моментов времени.
Рассмотрим прежде всего вопрос об определении длины и направления базиса.
Пусть известны высоты над уровнем моря и точные географические координаты - долготы и широты пунктов наблюдения - концов базиса. Один из них, О1, будем считать основным, а второй, О2, - вспомогательным. При фотографических наблюдениях в основном пункте обычно устанавливают фотокамеры, снабженные обтюратором.
Будем рассматривать из пункта O1 пункт O2. Направление O1O2 пересечет небесную сферу основного наблюдателя, находящегося в пункте О1 в точке O2. Нам надо определить ее экваториальные координаты па небесной сфере, описанной вокруг точки О1.
Рассмотрим пространственную прямоугольную систему координат, у которой начало поместим в центре Земли. Ось CZ направим вдоль оси вращения Земли, а ось СХ расположим в плоскости меридиана основного пункта наблюдений O1. Ось CY располагается в плоскости экватора под углом 90° к западу от осиСХ (рис. 119). Соединим пункт наблюдений Ог с центром Земли. УголXCO1 = φ называется геоцентрической широтой, а расстояние СO1 = ρ1 + h1 где h1 - высота пункта Ог над уровнем моря, а ρ1 - радиус-вектор Земли на широте φ. Эти величины связаны с географической широтой ср формулами
φ' = φ - 692",6 sin 2φ + ... (5.28)
и
ρ = 6378245 - 21201 sin2ρ' - 179 sin4ρ' + ... (метров). (5.29)
Опустим перпендикуляр O1Q из точки O1 на плоскостьXCY. Это даст возможность вычислить прямоугольные координаты точки О1:
x1 = (ρ + h1) cosφ1, y1 = 0 и z1 = (ρ1 + h1)sinφ1 (5.30)
Проделаем такое же построение из точки O2 (прямая O2N). Эта точка будет лежать в плоскости другого меридиана; если этот меридианРК' расположен к западу от основного меридианаРК, то угол между ними, равный углуКСК',равен разности долгот Δλ= λ1 - λ2, коль скоро долготы возрастают к востоку. Перпендикуляр, опущенный из точки O2 на плоскость экватораXCY, упадет в точкуN. Из рис. 119 видно, что отрезокCN равенCN = (ρ2 + h2) cosφ2, а отрезок NO2 = z2 = (ρ2 + h2)sinφ2/ (5.31)
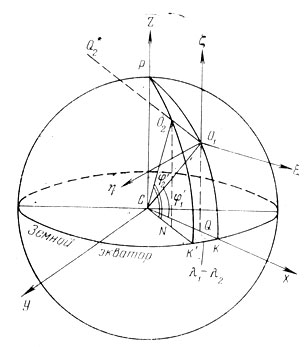
Рис. 119. К определению элементов базиса
Проектируя отрезокCN на осьОХ, находим
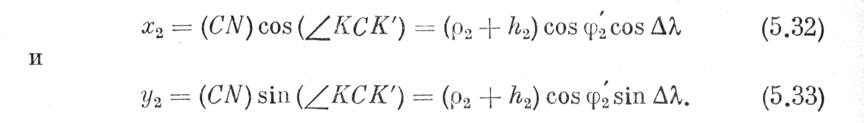
Теперь сделаем параллельный перенос осей координат из точки С в точку O1, где находится основной наблюдатель. Новые координаты будут таковы. Ось O1ζ направлена вдоль оси мира. Ось O1ξ расположится в плоскости небесного меридиана точки O1 и в плоскости небесного экватора, а ось О1η направлена в точку запада. Чтобы получить координаты пункта O2 в этой новой системе, надо образовать разности:
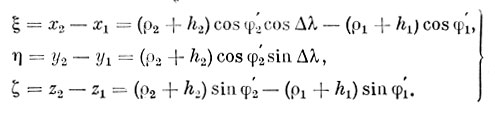
Однако эти формулы неудобны для осуществления вычислений по той причине, что в них заключены разности близких по значению величин; при выполнении таких вычислений всегда теряется точность. Поэтому мы их упростим. Обозначим ρ1 + h1= R, а ρ2 + h2 = R + ΔR. Тогда
ΔR = (ρ2 + h2) - (ρ1 + h1).
Далее обозначим φ2 = φ1 + Δφ'.
Начнем упрощения с формулы для η; пишем в новых обозначениях:
η = (R + ΔR)cos(φ1' + Δφ')sinΔλ.
Замечаем, что Δφ' и Δλ - малые величины. Следовательно, можно приближенно положить cos = Δφ = 1. Далее мы будем пренебрегать произведениями малых величин, если они не умножаются на такую большую величину, какR. Проследите за преобразованиями и тем, как мы отбрасываем очень малые величины, которые в формулах подчеркнуты:
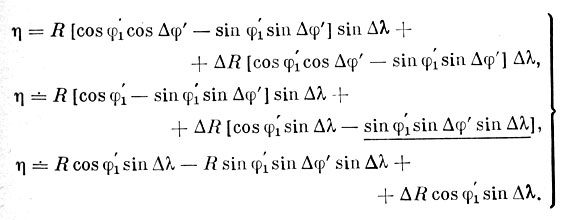
(5.35)
Точно так же преобразуем формулу для вычисления ζ:
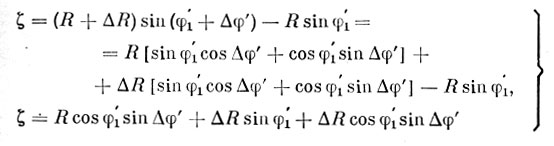
(5.36)
и формулу для вычисления ξ:
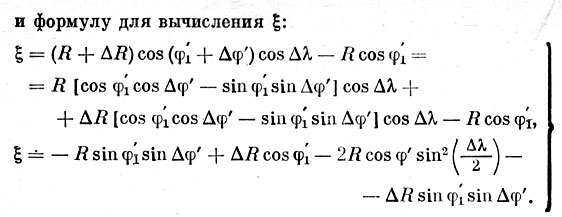
При обработке фотографических наблюдений надо воспользоваться полными формулами. При изучении визуальных наблюдений можно откинуть члены высших порядков малости и использовать формулы, в которых оставлен только первый член:
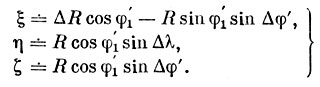
Теперь, зная, чему равны ξ, η и ζ, определяем длину базиса г по очевидной формуле:
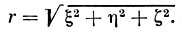
Чтобы получить экваториальные координаты точки O2, т. е. точки O2, рассматриваемой из точки О1, надо использовать формулы, которые легко выводятся и в которых приняты следующие обозначения:t*- часовой угол точки O2*, а δ*- ее склонение:
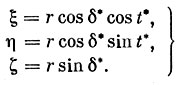
(5.40)
Из них выводятся окончательные формулы:
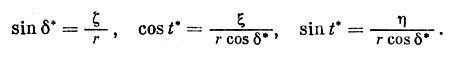
(5.41)
Вычислить придется как sint*,так и cost*,так как надо знать, в каком квадранте находится значениеt*.
И наконец, последнее: вследствие суточного вращения небесной сферы величина α* все время изменяется; она равнаα* = s - t*.


