


§ 74. Двойные звезды и звездные массы
Очень часто невооруженному глазу звезда кажется одиночной, но если посмотреть на нее в телескоп, даже не с очень большим увеличением, можно увидеть около нее спутника. Физическая двойственность звезды обнаруживается при очень длительных наблюдениях, когда становится заметным орбитальное движение. Обе компоненты двойной звезды обращаются по орбитам около центра масс системы, что проявляется в периодическом изменении угловых расстояний и по- 270е-зиционных углов, как это видно, например, из рис. 138.
Сейчас известно свыше 60 тысяч двойных звезд, из которых около двух тысяч обнаружили орбитальное движение. Вычислены элементы орбит свыше 500 двойных звезд.
Некоторые из двойных звезд не являются реальными звездными парами, связанными узами взаимного тяготения; это далекие друг от друга звезды, случайно оказавшиеся вблизи луча зрения. Такие двойные звезды называются оптическими и интереса для науки не представляют.
Кроме двойных, встречаются также и кратные звезды, состоящие из трех и более компонент. Такой, например, является е Лиры. Уже в бинокль она кажется двойной, но если посмотреть в телескоп при большом увеличении, то каждая из звезд разделяется еще на две, так что е Лиры - четверная система.
Звезда О Ориона окутана знаменитой туманностью. В телескоп звезда видна как трапеция, состоящая из четырех звезд. Известно, что одна из этих звезд, носящая название ВМ Ориона,- тесная двойная (затменная переменная) звезда. Кроме того, еще две звезды, по-видимому, принадлежат этой же трапеции, которая оказывается семикратной звездой. Кастор (ос Близнецов) также шестикратная звездная система. Таким образом, кратных звезд в природе много.
Двойные и кратные звезды - исключительно интересное и красивое зрелище. Очень часто яркая звезда желтая, а ее спутники - голубоватые или даже зеленоватые, благодаря контрасту; желтые и красные лучи яркой звезды утомляют глаз и он видит слабые спутники окрашенными в дополнительные цвета. Рекомендуем наблюдателю, располагающему хотя бы небольшим телескопом, посмотреть па двойные звезды таблицы XVI.
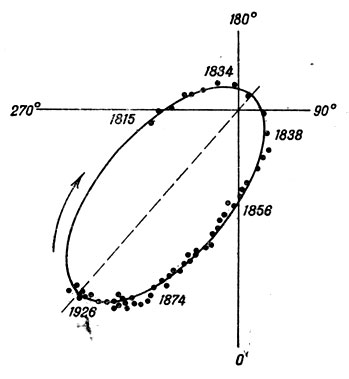
Рис. 138. Видимое движение двойной звезды
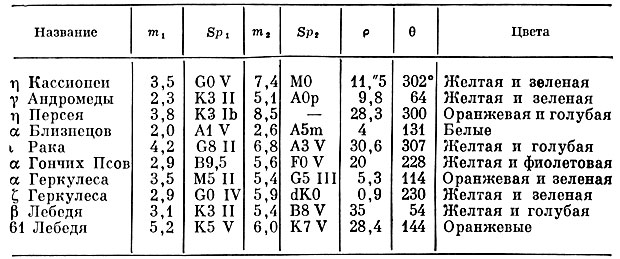
Таблица XVI. Интересные двойные звезды
В этой таблице указаны звездные величины mи спектральные классыSp компонент, угловое расстояние между компонентами ρ и позиционный угол θ.
Гораздо более полный список двойных звезд приведен в таблицах 55 и 56 «Справочника любителя астрономии» П. Г. Куликовского, «Наука», 1971 г.
Некоторые из помещенных в нашей таблице двойных звезд заслуживают особого внимания, так как у них обнаружены орбитальные движения, вычислены элементы орбит и определены периоды обращения. У двойной звезды η Кассиопеи период обращения Р = 526 лет, у α Близнецов Р = 420 лет, у ζ ГеркулесаР= 34,38 года и у 61 ЛебедяР = 692 года.
Из сопоставления этих чисел видно, что визуально-двойные звезды имеют большие периоды обращения. Самая «короткопе-риодическая» визуально-двойная звезда е Кита имеет период обращения, равный 2,62 года. И это неудивительно. Для этого чтобы раздельно видеть обе компоненты визуально-двойной звезды, надо, чтобы они были достаточно далеки друг от друга, а в таком случае и их орбитальные периоды велики. Существует очень много двойных звезд, имеющих гораздо более короткие периоды обращения, но они визуально не разделяются и их изучают другими способами.
Мы уже говорили, что обе компоненты описывают орбиты около общего центра масс, который расположен между ними на прямой линии, соединяющей обе компоненты, и делит их взаимное расстояние обратно пропорционально массам. Это сказывается на измерениях положений двойных звезд. При наблюдениях определяют угловое расстояние между компонентами р и позиционный угол 0, отсчитываемый от направления к северному Полюсу мира против часовой стрелки. Визуальные наблюдений сводятся к определению» положения спутника относительно главной звезды. Иное дело, если измерения проводятся на фотографических снимках, полученных длиннофокусным астрографом. В таком случае можно определить, «привязываясь» к окрестным звездам, движение каждой компоненты, найти положение центра масс системы и даже исследовать его поступательное движение на фоне звездного неба. Такие измерения гораздо ценнее, так как дают возможность определить орбиту каждой компоненты, а значит, вычислить и отношение их масс.
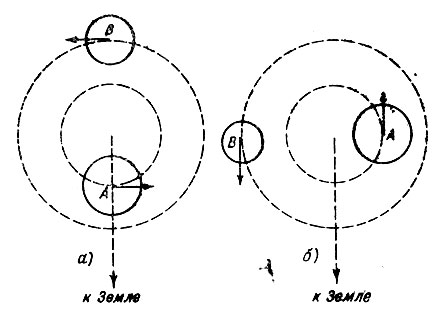
Рис. 139. Движения в системе спектрально-двойной звезды
Допустим теперь, что у двойной звезды спутник настолько слаб, что мы его не видим (может быть, это околозвездная массивная планета). Тогда главная звезда все равно будет описывать орбиту вокруг центра масс, и можно будет установить существование ее невидимого спутника. Такие открытия были сделаны несколько раз и впоследствии спутник находили в телескоп. Один же случай является совершенно исключительным. Пулковский астроном А. Н. Дейч, изучая движения, происходящие в системе двойной звезды 61 Лебедя, пришел к выводу, что у более яркой компоненты существует темный спутник, имеющий массу, близкую к 0,01 массы Солнца. Спутник движется по эллиптической орбите, у которой большая полуось равна трем астрономическим единицам, и совершает полный оборот вокруг центрального светила за 4,9 года. По-видимому, этот спутник является планетой.
Помимо визуальных двойных звезд известно большое число звезд, называемых спектрально-двойными. Рассмотрим, что должно происходить в такой двойной системе, если плоскость ее орбиты наклонена к лучу зрения под малым углом. На рис. 139 изображены два различных положения компонент по отношению к лучу зрения. В левой части рисунка обе компоненты движущийся перпендикулярно к лучу зрения и проекции их орбитальных скоростей на луч зрения равны нулю. По истечении четверти периода обращения компоненты займут положения, изображенные в правой части рисунка.
Компонента А будет удаляться от наблюдателя, ее лучевая скорость будет положительна, и все спектральные линии вследствие эффекта Доплера сдвинутся, пропорционально лучевой скорости в красную сторону спектра. Компонента В приближается к нам, и ее лучевая скорость отрицательна. Поэтому в ее спектре линии сдвинутся к фиолетовому концу спектра. Мы наблюдаем суммарный спектр обеих компонент. Поэтому в таком положении, какое изображено в правой части рис. 139, спектральные линии должны раздвоиться, что, действительно, во многих случаях и наблюдается.
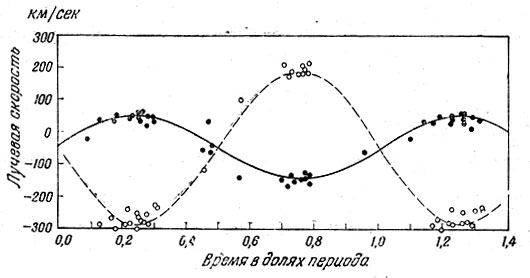
Рис. 140. Кривая изменения лучевых скоростей V502 Змееносца. Показаны скорости обеих компонент
Еще через четверть периода линии сольются, так как обе компоненты будут двигаться перпендикулярно к лучу зрения, а еще через четверть периода будет снова наблюдаться раздвоение линий, но теперь к нам будет приближаться компонента А, а удаляться компонента В.
Измеряя лучевые скорости и найдя период их изменения, астрономы изображают все данные на графике (рис. 140). На нем сплошной линией изображена кривая изменения лучевой скорости одной компоненты, а штриховой линией - другой. Такие звезды, у которых двойственность обнаруживается из изменений лучевых скоростей, называются спектрально-двойными.
Совершенно не обязательно, чтобы в спектре наблюдалось раздвоение линий. Может оказаться, что вторая компонента гораздо слабее первой и в суммарном спектре себя не проявляет. Все равно, спектральные линии будут смещаться и можно построить кривую изменения лучевой скорости одной компоненты, если только определить орбитальный период. Правда, как мы увидим дальше, в этом случае мы получаем гораздо более бедную информацию о двойной звезде, чем в случае раздвоения спектральных линий.
Посмотрим теперь, какие выводы можно сделать из кривых изменения лучевых скоростей? Для простоты рассуждений допустим, что орбиты компонент круговые и, следовательно, что обе они движутся с постоянными орбитальными скоростями. Предположим для начала, что луч зрения лежит в плоскости орбиты.
При движении компонент по орбитам угол между лучом зрения и направлениями скоростей звезд будет периодически изменяться, и потому лучевые скорости также должны испытывать периодические изменения. Наибольшие лучевые скорости будут наблюдаться при совпадении направления орбитальной скорости с направлением луча зрения. Таким образом, скорость звезды при ее движении по круговой орбите равна максимальной из наблюдаемых лучевых скоростей, или половине амплитуды изменения лучевой скорости. Установив значения двум кривым (как на рис. 140), мы можем приступить к дальнейшим вычислениям.
Так как при круговом движении орбитальная скорость постоянна, то длина орбиты будет равнаl = ν xP, где период Р надо выразить в секундах. С другой стороны, длина орбиты равна, где через обозначен радиус «абсолютной» орбиты, т. е. расстояние от звезды до центра масс системы. Итак, имеем
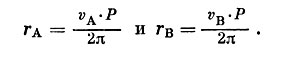
(7.14)
Теперь можно применить третий закон Кеплера:
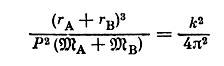
(7.15)
и определить сумму масс компонент
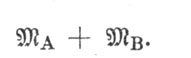
В данном случае имеется возможность определить массу каждой компоненты, так как известны радиусы их «абсолютных» орбит rA и rB и всегда выполняется соотношение
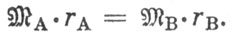
В случае эллиптических орбит вычисления выполняются гораздо сложнее, но принцип остается тем же самым, что и при круговых орбитах.
Теперь нетрудно видеть, что при наличии кривой лучевой скорости только одной компоненты такое полное решение невозможно и приходится делать мало обоснованные дополнительные предположения об отношении масс компонент.
При этих рассуждениях мы полагали, что луч зрения наблюдателя расположен в плоскости орбиты. Если же он наклонен к ней, то мы не можем вычислить ни υA, ни υB. Определяющая их формула теперь содержит множитель, вавйсящий от наклонения луча зрения к плоскости орбиты. Решение основной задачи определения масс осложняется, и одних спектральных наблюдений для этого недостаточно.
Теперь на помощь приходят затменные переменные звезды. В тех случаях, когда луч зрения мало наклонен к плоскости орбиты, компоненты при их орбитальном движении должны на время закрывать друг друга от наблюдателя и будут происходить затмения. В это время общий блеск двойной системы уменьшается. Таких звезд очень много. Первая из обнаруженных звезд этого типа - уже знакомый нам Алголь, звезда [В в созвездии Персея (см. § 1). Период изменения блеска, равный периоду орбитального движения, Р = 2,867 суток. Свойства затменных звезд будут описаны в главе VIII; здесь мы только заметим, что из кривой изменения блеска во время затмения определяется не только наклонение луча зрения к плоскости орбиты, но и размеры звезд. Очевидно, что затменные звезды являются также и спектрально-двойными, так как у них луч зрения мало наклонен к плоскости орбиты. Таким образом, сочетание спектральных и фотометрических наблюдений дает наиболее полный ответ на большинство поставленных вопросов.
Зная массы и радиусы, можно вычислить средние плотности их вещества. Для этого достаточно разделить массу на объем. И это привело к многим важным открытиям, о которых мы сейчас и расскажем.


