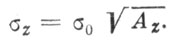Дополнение I. Способ наименьших квадратов
Очень часто астрономам приходится решать следующую задачу. Пусть дано несколько уравнений, содержащих две неизвестные величины и имеющих вид
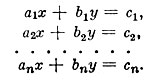
Здесь из измерений известны величины а1, а2, ... аn; b1, b2, b3, ..., bn; c1, c2, ..., cn и неизвестны x и y.
Надо решить эту систему уравнений. Если бы эти уравнения были совершенно точными, то не было бы необходимости в таком количестве уравнений - было бы достаточно только двух. Вопрос осложняется тем обстоятельством, что каждое уравнение получено из измерений, а всякое измерение неизбежно содержит случайную ошибку. Поэтому уравнения должны быть заменены следующими:
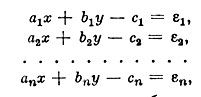
где ε1 ε2, . . . , εn - неизвестные нам ошибки измерений. Такие уравнения называются условными.
Эту систему уравнений решить обыкновенными приемами невозможно, так как она содержит n + 2 неизвестных: x, у, ε1, ε2, . . ., εn. Поэтому решают ее другим приемом, который называется способом наименьших квадратов. Мы не можем дать полного обоснования этого способа, так как для этого необходимо знание высшей математики, но все же его основную идею понять нетрудно.
Для простоты предположим, что у нас имеется два основных неизвестных х и у. Вычислим квадраты ошибок εj и сложим их друг с другом. Мы получим сумму квадратов всех отклонений
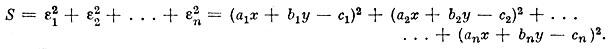
Естественно считать наилучшими значениями неизвестных х и у такие, при которых сумма квадратов ошибок S наименьшая. Такие значения называются наивероятнейшими, а способ их отыскания - способом наименьших квадратов.
Преобразуем выражение S, раскрыв скобки и объединив подобные члены:
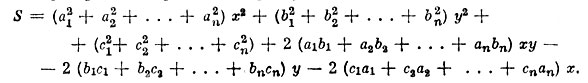
Для краткости обозначим коэффициенты так:
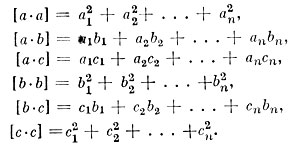
Все эти коэффициенты известны из уравнений и при изменении х и у не изменяются. Итак,
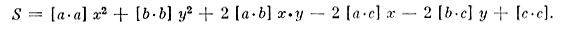
Наша дальнейшая задача состоит в том, чтобы найти значения х и у, при которых S было бы наименьшим.
Рассмотрим сначала более простую задачу. Пусть некоторая величина w зависит от переменной величины z следующим образом:
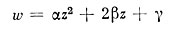
и требуется найти наименьшее значение w. Выделим в w полный квадрат:
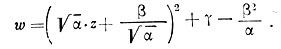
Значение w становится наименьшим, когда выражение в скобке равно нулю и, следовательно,
az + β = 0.
Возвращаясь к решению нашей задачи, запишем величину S следующим образом:
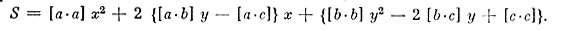
Оставляя у неизменным, мы теперь легко убеждаемся в том, что S принимает наименьшее значение при х, удовлетворяющем уравнению
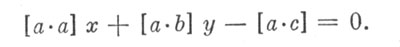
Это уравнение называется первым нормальным уравнением. Аналогично, переписав по-новому выражение S, оставляя неизменным х и разыскивая наименьшее значение S при переменном у, мы придем ко второму нормальному уравнению:
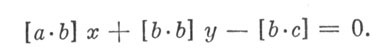
Итак, вероятнейшие значения x и у, при которых S имеет наименьшее значение, получаются из двух нормальных уравнений:

Эта система уравнений решается обычными приемами алгебры.
Полное развитие способа наименьших квадратов дает возможность вычисления не только вероятных значений неизвестных величин ж и у, но и их вероятных ошибок. Можно легко обобщить способ наименьших квадратов и на такие условные уравнения, которые содержат любое число неизвестных величин х, у, z ...
Пример. Пусть из наблюдений блеска звезд получена степенная шкала: a = 0,0; b = 8,8; с = 12,9; d = 16,6. Далее оказалось возможным получить из фотометрического каталога звездные величины: mа = 8m,53; mb = 9m,00; mс= 9m,30; md=9m,56. Требуется найти формулу, связывающую степени и звездные величины. Обозначая значение степени через р, а звездную величину, соответствующую блеску 0,0 степеней,- через то, можно получить общий вид формулы
m = mо + Р x s,
где s - число степеней, измеряющих блеск данной звезды в полученной шкале. Используя наши данные, получаем систему уравнений:
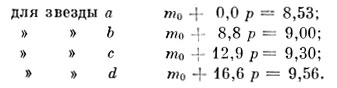
Все эти уравнения получены из наблюдений и потому неточны; мы называем их условными. Надо составить нормальные уравнения и решить их относительно неизвестных m0 и р. Выписываем колонки коэффициентов:
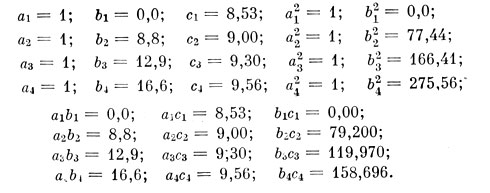
Суммируя, находим
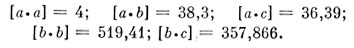
Получаем нормальные уравнения, несколько округлив коэффициенты:
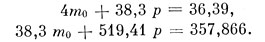
Решая, находим m0 = 8,51, р = 0,0618. Итак, вероятная формула имеет такой вид:
m = 8,51 + 0,0618 s.
Подставляя наблюденные значения s, получаем исправленные значения звездных величин звезд сравнения в соответствии со шкалой. Сводим все вместе в одну табличку:
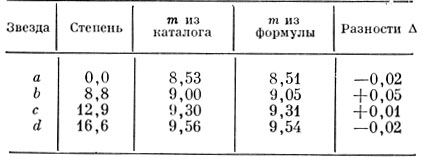
Таблица
Если вычисления выполнены верно, то сумма всех разностей, которые показаны в последней колонке, должна быть близка к нулю. В нашем случае так оно и есть.
Конечно, мы привели частный пример использования способа наименьших квадратов. Он широко применяется и при решении других задач. Аналогичные вычисления делаются при улучшении периодов переменных звезд.
Скажем в заключение несколько слов о том, как вычислить вероятные ошибки неизвестных. Для этого надо подставить полученные значения неизвестных во все условные уравнения и найти остающиеся отклонения Δ. В предыдущем примере они указаны в столбце «разности». Затем надо найти сумму квадратов остающихся отклонений [Δ.Δ]. В пашем примере она равна
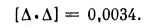
Полученную сумму надо разделить на число условных уравнений n, из которого вычитается число неизвестных величин k и извлечь квадратный корень. Тогда ошибка единицы веса будет
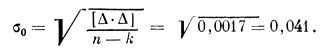
Чтобы найти квадратичные ошибки неизвестных, надо решить такие уравнения:
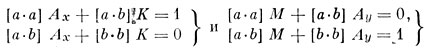
и определить из них величины Ах и Ау(К и М определять не нужно). В нашем примере решаем уравнения:
и получаем величины:
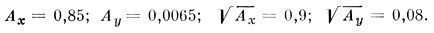
Квадратичные ошибки неизвестных определяются из формул
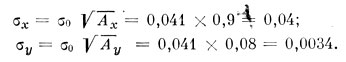
Итак, решение наших условных уравнений имеет вид
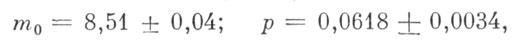
и формула часто записывается в таком виде:
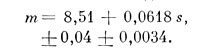
Приведем без вывода все необходимые сведения для решения условных уравнений
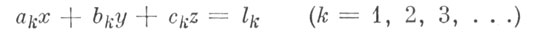
с тремя неизвестными по способу наименьших квадратов. Нормальные уравнения имеют такой вид:
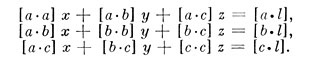
Их решение дает значения х, у к z.
Далее вычисляются отклонения Δ и находится ошибка единицы веса
по формуле (I,1), где надо принять k = 3.
Для определения квадратичных ошибок неизвестных надо решить три системы уравнений. Первая из них
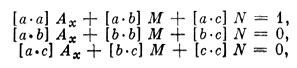
решается относительно Ах, и тогда
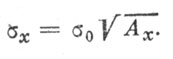
Вторая система
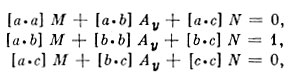
решается относительно Aу и
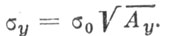
И, наконец, третья система имеет вид
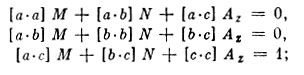
ее решают относительно Аz и находят