


§ 16. Перевод среднего времени в звездное и обратно
Для определения среднего времени нет необходимости прибегать к наблюдениям Солнца, описанным в § 14. Его можно вычислить по звездному времени, которое определяется из наблюдений точнее. Можно также, зная среднее время, вычислить звездное. Покажем, как это делается.
Начнем с преобразования промежутков времени. Обозначим промежуток времени между двумя событиями через τ. Если разделить т на продолжительность средних сутокТ, то мы получим величину τm, показывающую, чему равен промежуток т, выраженный в единицах среднего времени. Итак, τm = τ/Т. Аналогично разделим т на продолжительность звездных суток S и получим величину τs - промежуток т, выраженный в единицах звездного времени: τs = τ/T, откуда
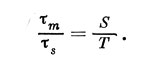
Теперь надо вычислить отношение S/T. Мы уже говорили, что год содержит 365,2422 средних солнечных суток. Так как за год «среднее солнце», двигаясь с запада на восток, т. е. против суточного вращения небесной сферы, делает один полный обход по экватору, то за это время небесная сфера сделает на один суточный оборот больше, чем Солнце. Таким образом, год содержит 366,2422 звездных суток и равен
Е=365,2422Т=366,2422S
Отсюда находим
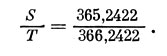
Сравнивая с предыдущей формулой, получаем
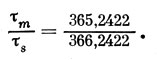
Последнее соотношение позволяет переводить интервалы времени. Чтобы получить величину тт по заданной величине ts, преобразуем последнюю формулу следующим образом:
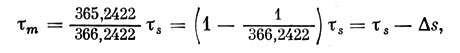
где
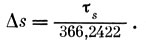
Эта поправка Δs легко находится по таблице 2 (стр. 369), в которой она указана для часов, минут и десятков секунд звездного времени. Покажем на примере, как пользоваться этой таблицей. Допустим, что нам надо выразить 14 ч. 46 м. 54 с. звездного времени в единицах времени среднего. Из таблицы 4 находим величину Δs:

Вычитая затем As из ts, находим тт в соответствии с формулой:
τm = τ s- Δs = 14 ч. 46 м. 54 с. - 2 м. 25,3 с. = 14 ч. 44 м. 28,7 с.
Для решения обратной задачи, превращения интервала среднего времени tm в интервал звездного времени, перепишем исходную формулу в следующем виде:
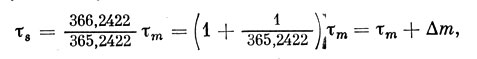
где через Δm обозначена величина
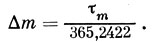
Значения ;поправок Δm приведены в таблице 3 (стр. 369).
Приводим пример использования этой таблицы. Пусть дано τm = 18 ч. 24 м. 35 с. среднего времени и надо найти соответствующий ему интервал звездного времени τs. Находим по таблице 4:
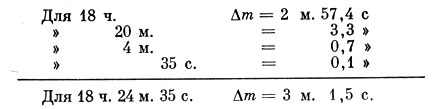
Итак, τs=τm+ Δm=18 ч. 24 м. 35 с. +3 м. 1,5 с. = 18 ч. 27 м. 36,5 с.
Теперь можно приступить к решению полной задачи. Допустим, что нам известно звездное время в некоторый момент и нам надо найти среднее время. Например, пусть в пункте с долготой λ = 2 ч. 3 м. О с. астроном наблюдал звезду а Орла, имеющую прямое восхождение α = 19 ч. 48 м. 20 с. (для эпохи 1949 г.), 16 августа 1949 г. в момент ее верхней кульминации. Нужно определить среднее местное время.
Мы знаем, что звездное время равно прямому восхождению кульминирующей звезды. Поэтому заданная нам задача сводится к определению момента среднего времени, соответствующего звездному времени 19 ч. 48 м. 20 с. 16 августа 1949 года.
Прежде всего узнаем, каково было звездное гринвичское время sгр в этот момент. Для этого надо отнять долготу. Получаем
sгр=s- λ=19 ч. 48 м. 20 с. -2 ч. 3 м. 0 с. = 17 ч. 45 м. 20 с.
Как мы увидим в следующем параграфе, в «Астрономическом Ежегоднике» приводятся значения звездного времени для нуля часов всемирного времени для каждого дня года s0. Находим из Ежегодника 1949 г. значение s0 для 16 августа; оно равно s0 = 21 ч. 36 м. 13 с. Это позволяет найти интервал звездного времени τs, протекший с момента гринвичской полночи, т. е. τs = sгр-s0
В нашем случае
τs=17 ч. 45 м. 20 с. - 21 ч. 36 м. 13 с.= -3 ч. 50 м. 53 с.
Остается преобразовать ts в тт, как уже было объяснено, для того, чтобы получить интервал среднего времени, протекший с момента гринвичской полночи, т. е. всемирное время. Находим по таблице 3 поправку Δs = 38 с. Отсюда τm = - 3 ч. 50 м. 15 с. = Тгр - среднее гринвичское (или всемирное) время. Для получения среднего местного времени прибавляем долготу:
Таким образом, мы получили, что в момент верхней кульминации α Орла местное среднее время было равно 22 ч. 12 м. 45 с.
Если бы нам надо было получить поясное время, то к Тгр надо было бы прибавить не долготу, а номер часового пояса N. Мы получили бы
Тпоясн=Тгр+N= -3 ч. 50 м. 15 с.+2ч.= -1ч. 50 м. 15 с.=22 ч. 09 м. 45 с.
Для получения же декретного времени надо прибавить еще один час:
Тдекр = Тпоясн + 1 ч. = 23 ч. 09 м. 45 с.
Теперь решим обратную задачу. Дано среднее местное время в пункте с долготой λ = 2 ч. 30 м. 18 с., равное Тт = 1949, августа 16, 14ч. 18 м. 44 с. Надо узнать, чему равно звездное время в этот момент. Начинаем с того, что находим всемирное время Тгр = Тm - λ = - 14 ч. 18 м. 44 с. - 2 ч. 30 м. 18 с. = 11 ч. 48 м.26 с. Очевидно, что Тгр равно интервалу среднего времени, протекшему с момента гринвичской полночи, и эту величину можно обозначить через λm. Найдем теперь, сколько прошло звездного времени с момента гринвичской полночи, для чего превращаем λm в λs. Находим по таблице 3 поправку Δm = 1 м. 56 с-, и получаем
τs=τm+Δm=11 ч. 48 м. 26 с. + 1 м. 56 с. = 11 ч. 50 м. 22 с.
Остается прибавить к полученной величине s0 - звездное время в среднюю гринвичскую полночь, взятое из Ежегодника:
sгр=s0+τs= 21 ч. 26 м. 13 с. + 11 ч. 50 м. 22 с. = 33 ч. 26 м. 35 с. = 9 ч. 26 м. 35 с.
Для получения же местного звездного времени надо добавить еще и долготу:
s =sгр+λ=9 ч. 26 м. 35 с. + 2 ч. 30 м. 18 с. = 11 ч. 56 м. 53 с.
По этому способу решаются все соответствующие задачи.


