


§ 21. Основы сферической тригонометрии
Теперь мы переходим к более сложным вопросам, связанным с выполнением математических расчетов. Читатель, чувствующий себя недостаточно подготовленным, может пропустить §§ 21-25.
Решение ряда задач сводится к вычислениям сторон и углов треугольников, расположенных на сфере. Пусть на небесной сфере выбраны три точки А, В и С. Соединим их дугами больших кругов; образуется сферический треугольник (рис. 46).
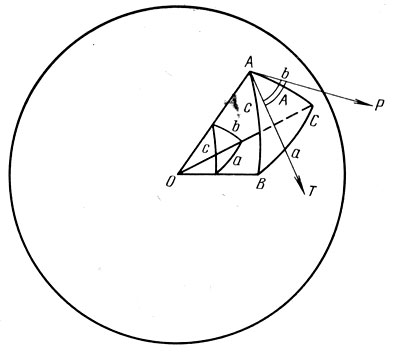
Рис. 46. Элементы сферического треугольника
Для того чтобы определить понятие об угле между сторонами сферического треугольника, проведем касательные к сторонам в точке их пересечения, т. е. в вершине угла. На рис. 46 - это прямые АР и AT, a угол А сферического треугольника (угол между сторонами АВ и АС) определяется углом ∠ТАР между касательными АР и AT.
Стороны сферического треугольника обозначаются малыми буквами a, ft и с, причем обозначения выбираются так, чтобы против угла А располагалась сторона а, против угла В - сторона ft и против угла С - сторона с. Очевидно, что стороны треугольника измеряются центральными линейными углами. Сторона а измеряется углом между радиусами сферы ОС и 0В, сторона ft измеряется углом между ОС и ОА и сторона с - углом ∠АОВ.
Существуют три группы формул, которые связывают между собой стороны и углы треугольника. Первая группа:
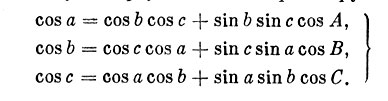
(2.2)
Эта группа формул позволяет легко вывести вторую группу:
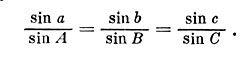
(2.3)
Это так называемая формула синусов.
Часто пользуются еще одной группой формул, которые также выводятся из формул (2.2):
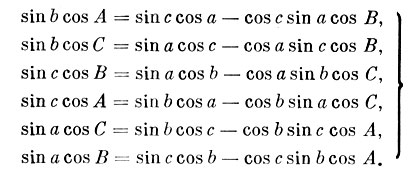
(2.4)
Каждая из входящих в эту группу формул называется формулой пяти элементов, так как в нее входят три стороны и два угла.
Конечно, этими тремя группами формул все содержание сферической тригонометрии не исчерпывается, однако для наших целей их вполне достаточно.


