


§ 22. Преобразование горизонтальных координат в экваториальные и обратно
На основе главных точек горизонтальной и экваториальной систем координат строится так называемый первый астрономический треугольник. Рассмотрим рис. 47, на котором изображены обе системы координат - горизонтальная и экваториальная. Сферический треугольник PZQ, который также изображен в правой части рис. 47, образован дугами больших кругов - меридиана PZ, вертикала светила ZQ и круга склонения PQ.
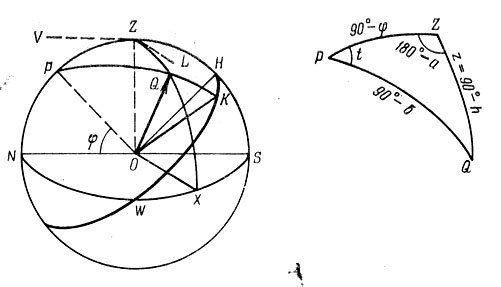
Рис. 47. Небесная сфера с первым астрономическим треугольником
Его стороны: ZQ - зенитное расстояние светила z = 90° - h, PQ - полярное расстояние р = 90° - δ точки Q, а PZ дополняет до 90° дугу PN', которая^, как известно, равна географической широте ф места наблюдения, так что PZ - 90° - φ.
Угол Р, как нетрудно видеть, равен часовому углу t. Что касается угла Z, то его определить несколько сложнее. Это угол между касательными ZV и ZL\ он одновременно измеряется дугой горизонта NX, которая равна разности дуг NS = 180°,и SХ = а - азимуту светила. Таким образом, Z = 180° - а. Третий угол треугольника, с вершиной в точке Q, употребляется при вычислениях сравнительно редко; он называется параллактически углом,
Применение к этому треугольнику формул (2.2) - (2.4) позволяет переходить от одной системы координат к другой.
Теперь нам предстоит решить две задачи. Зная широту места наблюдения ф, зенитное расстояние z и азимут а светила, вычислить его часовой угол t и склонение δ.
Применим к стороне PQ первую формулу (2.2):
cos (90о- δ) = cos (90о-φ) cos z + sin (90о-φ) sin zcos (180о-а).
Использовав простейшие формулы приведения, найдем
sin δ = sin φcos z - cos φsin z cos а. (2.5)
По этой формуле, как мы поясним это примером, можно определить склонение светила δ.
Чтобы определить часовой угол t, применим формулу (2.3):
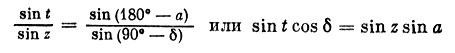
и, конечно,
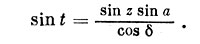
(2.6)
Хотя эта формула позволяет определить sint, найти по ней значениеt (однозначно) нельзя, так как одному и тому же значению синуса отвечают два значения:t и 180° -t. Надо узнать, чему равен cost. Для этого применим формулу (2.4) к сторонеPQ и углуР:
sin (90о-δ) cos t = sin (90о-φ) cos z - cos (90о-φ) sin z cos (180о - а)
или
cos δ cost = cos φ cos z + sinφ sin z cos а.(2.7)
Приводим пример численного решения задачи. Для выполнения вычислений понадобится арифмометр. Их можно, конечно, делать и по таблицам логарифмов, но это более громоздко. Итак, даны: широта места наблюдения φ = 51°37',3, зенитное расстояние светила z = 41°18',5 и азимут а = 38°18',4.
Найти склонение б и прямое восхождение а светила, зная, что в момент наблюдения звездное время а = 16 ч. 44 м. 52 с.
Выполняя расчеты, астроном обычно создает схему вычислений, программу. Можно предложить следующую схему: в первых ее двух строках выписаны синусы и косинусы исходных данных, взятые из пятизначных таблиц натуральных зйачений; в следующих строках указаны знаки действий, в соответствии с выведенными формулами:
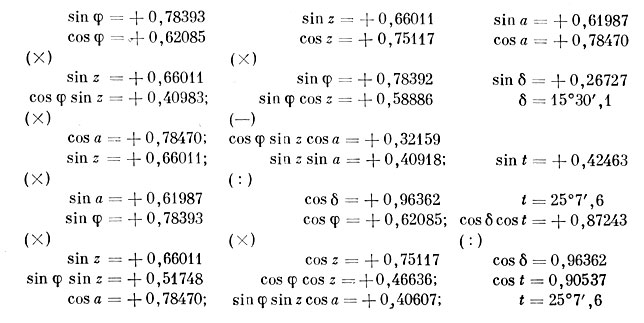
При выполнении этих вычислений нам пришлось интерполировать табличные величины, и округлять числа при умножении и делении.
Правила округления дробных частей чисел таковы. Например, если мы желаем из дроби 0,375648 получить округленное до пяти знаков значение, то, отбрасывая 8, мы должны к предпоследнему знаку добавить единицу, т.е. записать 0,37565. Если же округляется дробь 0,375644, то последняя цифра отбрасывается, так что нужно взять 0,37564. В тех случаях, когда в отбрасываемом знаке стоит цифра 5, условились округлять до четной цифры, т.е. число 0,375645 округляется так: 0,37564, а число 0,375635 также записывается как 0,37564.
Необходимость округления дробей вызвана следующим обстоятельством. Каждая из них является приближенным числом и его погрешность может достигать пяти единиц отброшенного знака. Вместе с тем арифмометр, при умножении, например, 0,62085 на 0,66011 дает ответ 0,4098 292 935. Конечно, такое количество цифр писать бессмысленно. Верных цифр только пять, и надо взять округленное значение дроби 0,40983, что мы и сделали выше.
В нашей схеме мы получили два значения t. Чтобы узнать, в каком квадрате находится t, необходимо определить знаки синуса и косинуса. В нашем случае они положительны и ответ надо поместить в первый квадрант, т. е. t = 25°7',6.
С другой стороны, два значения t, получаемых почти независимо, позволяют контролировать правильность выполнения вычислений. Вообще говоря, астрономы, составляя схемы вычислений, стараются ввести в них «посторонние» действия, которые автоматически контролировали бы правильность хода расчетов. Теперь превращаем часовой угол из градусной меры во временную и находим, что t = 1 ч. 41 м. 44 с. Так как α = s - t, то α = 16 ч. 44 м. 52 с.- 1 ч. 41 м. 44 5.= 15 ч. 03 м. 08 с.
Теперь приступим к решению обратной задачи. Нам даны φ, t и δ. Надо найти z и а.
Применим к треугольнику PQZ те же формулы сферической тригонометрии. Первую формулу (2.2) применим к стороне ZQ и найдем:
cos z = cos(90о-δ) cos(90о-φ) + sin(90о-δ) sin(90о-φ) cos t или cos z = sin δ sinφ+cosδcosφcost (2.8)
Формула (2.6) сохраняет свой смысл и в этом случае. Она переписывается так:
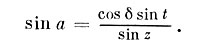
Чтобы определить, в каком квадранте расположено значение а, надо использовать одну из формул (2.4), применив ее к стороне ZQ и углу Z:
sin z cos (180о-а) = sin (90о - φ) cos (90о - δ) - cos (90о - φ) sin (90о - δ) cos t
или
sin z cos а = - cosφ sin δ+sinφcosδ cost. (2.10)
Задача решена и остается вычислить пример.
Дано: широта места равна 51°37',3. Часовой угол светила равен t = 22 ч. 40 м. 51 с., а склонение светила δ = -15°43',6. Вычислить зенитное расстояние и азимут.
Прежде всего превращаем t из временной меры в угловую:
t = 22 ч. 40 м. 51 с. = 340о12',8 = - 19о47',2.
Затем составляем наиболее удобную и краткую схему вычислений:
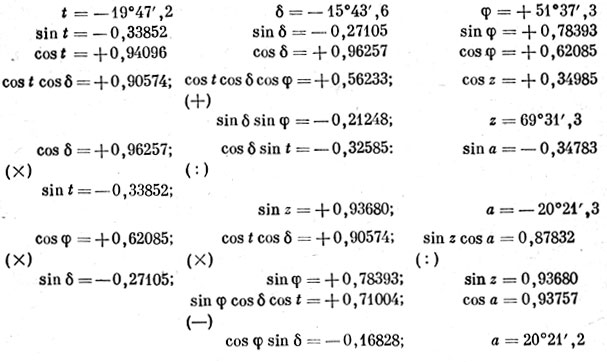
Мы нашли, что синус а отрицателен, а косинус а положителен. Следовательно, азимут расположен в четвертом квадранте и окончательный ответ таков: a = -20°21'3, z = 69°31'3.
Решим теперь такую задачу; определить время восхода или захода светила, зная его экваториальные координаты.
В самом деле, в момент восхода (или захода) зенитное расстояние должно быть равно 90°, если, конечно, пренебречь сравнительно небольшим влиянием рефракции света в земной атмосфере. Дело в том, что преломление света, происходящее в воздухе, приподнимает светило над горизонтом, т. е. уменьшает его зенитное расстояние. Вблизи зенита влияние рефракции очень мало, оно растет по мере увеличения зенитного расстояния. Однако даже на горизонте оно достигает всего половины градуса и при наших расчетах им можно пренебречь.
Приняв, что z = 90°, так что cos z = 0, подставим это значение в формулу (2.8) и найдем часовой угол t0:
cos tо = - tg δ х tg φ. (2.11)
Зная косинус t0, мы получим два значения угла: +t0 для точки захода и -t0 для восхода. Если нам известно прямое восхождение светила а, то мы найдем звездное время как восхода, так и захода по формулам:
sвосх = α - t0 и sзах = α + t0.
Остается только найти среднее время по известному звездному. Приводим численный пример: на этот раз мы воспользуемся логарифмами. Найдем, когда взошел и зашел Сатурн 4 ноября 1949 г. в пункте, имеющем географические координаты λ = 2 ч. 03 м. О с.: φ = +-46°29'0.
Из «Астрономического календаря» на 1949 г. находим экваториальные координаты Сатурна для 4 ноября 1949 г.: α = 11 ч. 13 м. 54 с.; δ = 6°52'.
Находим часовой угол точек восхода и захода по формуле (2.11), использовав для этого десятичные логарифмы:

Значокn появился потому, что в формуле стоит знак минус; это означает, что ответ отрицателен. По логарифму косинуса находим из таблиц угол 82°43'.
Так как косинус отрицателен, то tQ = 180° - 82°43' = 97°17'. Переведя его значение во временную меру, получаем
t0 = 6 ч. 29 м. 08 с.
Итак,
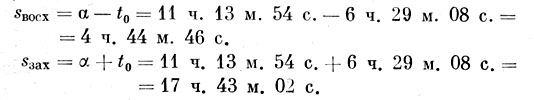
Остается последнее: перевести звездное время в среднее. Вычисляем параллельно:

Итак, 4 ноября 1949 г. Сатурн взошел в 2 ч. 50 м. и зашел в 15 ч. 46 м. по декретному времени пункта, расположенного во втором часовом поясе.


