


§ 24. Третий астрономический треугольник
Для целей статистического изучения звезд и туманностей бывает нужно вычислить галактические координаты, зная экваториальные. Покажем, по каким формулам это можно сделать.
На рисунке 45 была изображена галактическая система координат. Третий астрономический треугольник имеет вершины в следующих точках: в полюсе мира Р, северном галактическом полюсе F и светиле Q. Определим элементы этого треугольника. Сторона ГР - полярное расстояние галактического полюса и дополняет его склонение δ0 до 90°. Поэтому она равна 90° - δ0.
Сторона PQ - полярное расстояние светила р = 90° - δ. Сторона FQ - угловое расстояние светила от галактического полюса, т. е. 90° - b, где b - галактическая широта светила.
Теперь определим углы треугольника FPQ. Угол при точке F измеряется дугой галактического экватора MR, которая равна разности дуг АК = 90° и AM = Z', причем l = I - 33°, а I - галактическая долгота. Таким образом, угол Г = 90° - l'.
Несколько труднее определить угол Р. Он измеряется дугой небесного экватора NH', которая складывается из дуги АН' = 90° и дуги AN. Последняя же равна разности прямых восхождений светила (а) и точки А, в которой галактический экватор пересекает небесный экватор. Итак, ∠Р - 90° + а - а,а = 90° + а -282° = а - 192° (прямое восхождение точки А равно 282°; см. § 20). Все эти значения показаны на правой части рис. 45.
Применив к третьему астрономическому треугольнику формулы сферической тригонометрии, после упрощений мы получим:
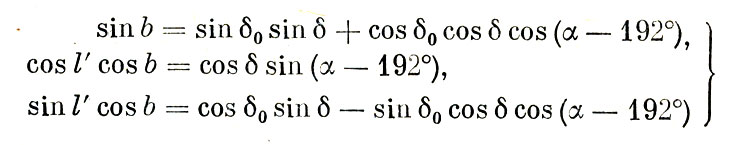
Если воспользоваться таблицами, облегчающими преобразование экваториальных координат в галактические (см. «Справочник астронома-любителя» П. Г. Куликовского, изд. 4-е, «Наука», 1971, стр. 570-575), то можно избежать вычислений по этим формулам, так как достаточно ограничиться приближенными значениями галактических координат.


